Your Ultimate Guide to the Matrix Determinant Calculator

Working with matrices can be complex. Whether you’re a student tackling linear algebra for the first time, an engineer solving intricate systems of equations, or a data scientist manipulating large datasets, matrix calculations can be tedious and prone to error. This is where a powerful online tool becomes indispensable. Our comprehensive matrix determinant calculator is designed to simplify these operations, providing you with a robust and user-friendly platform for all your matrix needs.

This article will walk you through every feature of our powerful tool. We’ll explore how it functions as more than just a determinant calculator, acting as a complete matrix solver for various operations. From addition and subtraction to multiplication, finding the determinant, and transposing matrices, you’ll see how this tool can save you time and improve your accuracy. We will cover each of the five main sections, explaining the inputs, outputs, and the step-by-step calculations displayed on the screen.

Matrix Addition Made Simple

The first function of our versatile tool is matrix addition. This fundamental operation has strict rules: you can only add matrices that have the exact same dimensions. Our calculator handles this requirement seamlessly, making the process straightforward.

How to Use the Addition Feature

When you navigate to the addition section of the matrix determinant calculator, you’ll find an intuitive interface.

• Inputs: The first thing you need to do is define the size of your matrices. You will see input fields for “Rows” and “Columns.” Enter the desired dimensions for Matrix A and Matrix B. The tool ensures both matrices will have the same size, as this is a requirement for addition.
• Editable Grids: Once you set the dimensions, two grids appear, labeled “Matrix A” and “Matrix B.” These grids are interactive, allowing you to click on each cell and type in your numerical values. This visual representation makes it easy to input your data without mistakes.
• Controls: Below the grids, you’ll find two primary buttons: “Calculate” and “Clear.” Clicking “Calculate” will perform the addition. The “Clear” button is a handy feature that resets all the cells in both matrices, allowing you to start a new problem without manually deleting each entry.
• Result and Steps: After you press “Calculate,” the results are displayed instantly. You will see the final “Sum Matrix,” which is the result of adding Matrix A and Matrix B. What makes this tool exceptionally helpful, especially for students, is the detailed “Steps” section. It shows the calculation for each element of the resulting matrix, such as C(1,1) = A(1,1) + B(1,1), providing complete transparency.
• Help Box: If you’re ever unsure about the rules of matrix addition, a “Help” box is available. It provides a quick refresher, explaining that matrices must have the same dimensions and that addition is performed by adding corresponding elements.

This section of the matrix determinant calculator transforms a potentially confusing task into a simple one, giving you both the answer and the understanding of how it was reached.

Effortless Matrix Subtraction

Similar to addition, matrix subtraction requires the matrices to have identical dimensions. The subtraction section of our tool mirrors the simplicity and functionality of the addition feature, ensuring a consistent and user-friendly experience.

Performing Subtraction with the Calculator

The layout and process for subtraction are designed for clarity and ease of use.

• Inputs and Grids: Just like with addition, you start by specifying the number of rows and columns. The tool will then generate two editable grids for Matrix A and Matrix B, ready for your data.
• Buttons: The “Calculate” and “Clear” buttons function in the same way. “Calculate” executes the subtraction of Matrix B from Matrix A, while “Clear” wipes the grids for a fresh start.
• Results Display: Upon calculation, the “Difference Matrix” is displayed. This is your resulting matrix. Alongside it, the “Steps” section breaks down the process element by element. It shows, for example, that the new element C(1,1) is found by A(1,1) - B(1,1). This step-by-step visibility is perfect for checking your work or learning the procedure.
• Helpful Guidance: A “Help” box is also present in this section, offering a concise explanation of matrix subtraction rules. It reminds you that the dimensions must match and that the operation involves subtracting the elements of the second matrix from the corresponding elements of the first.

This part of our matrix determinant calculator is another example of how we prioritize learning and verification alongside quick computation.

Mastering Matrix Multiplication

Matrix multiplication is significantly more complex than addition or subtraction. The rules for dimensions are different, and the calculation process is more involved. Our matrix determinant calculator is built to handle these complexities, making it a reliable tool for this tricky operation.

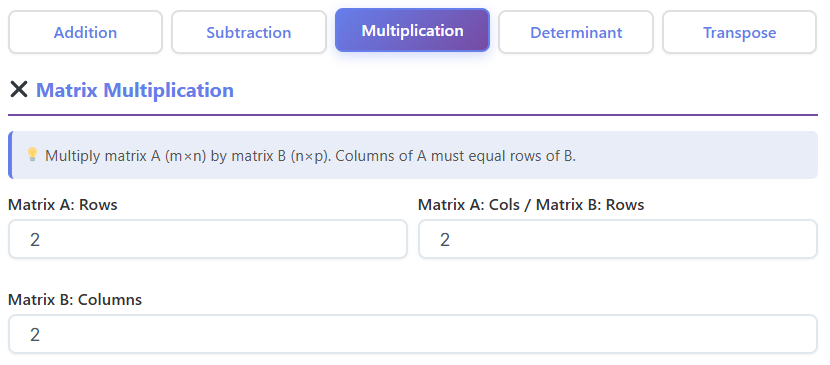
How the Multiplication Feature Works

The interface is specially adapted to the unique rules of matrix multiplication.

• Dimension Inputs: The rule for multiplication is that the number of columns in the first matrix (Matrix A) must equal the number of rows in the second matrix (Matrix B). The calculator’s input fields reflect this. You’ll specify the “Rows” and “Columns” for Matrix A, but for Matrix B, you only need to input the number of “Columns.” The number of rows for Matrix B is automatically matched to the number of columns from Matrix A.
• Editable Matrices: As before, two grids appear for you to enter the elements of Matrix A and Matrix B.
• Key Metrics: Before you even calculate, the tool provides useful metrics. It displays the sizes of both matrices (e.g., Matrix A: 3×2, Matrix B: 2×4) and tells you the size of the resulting matrix (in this case, 3×4). It also shows the “Total operations count,” which indicates the number of multiplications and additions required. This is great for understanding the computational effort involved.
• Detailed Steps: The “Steps” section in the multiplication feature is incredibly detailed. It breaks down how each element of the result matrix is calculated. For instance, to find the element in the first row and first column of the product matrix, it shows the dot product of the first row of Matrix A and the first column of Matrix B, with all the multiplication and addition steps written out.
• Result Matrix: Finally, the complete “Result Matrix” is displayed clearly at the bottom.

This section elevates the tool from a simple calculator to a powerful matrix solver, capable of guiding you through one of the most challenging matrix operations. Using this feature of the matrix determinant calculator can solidify your understanding of the multiplication process.

Finding the Determinant of a Matrix

The determinant is a special number that can be calculated from a square matrix. It has many applications in linear algebra, from determining if a system of linear equations has a unique solution to finding the inverse of a matrix. Our tool includes a specialized determinant calculator function for this purpose. Many users search for how to find the determinant of a matrix, and this tool provides the answer instantly.

Using the Determinant Calculator Function

This section is dedicated solely to calculating the determinant for 2×2 and 3×3 matrices.

• Matrix Size Input: The first step is to choose the size of your square matrix. You can select either “2×2” or “3×3” from a simple dropdown menu.
• Matrix Grid: An editable grid corresponding to your chosen size will appear, allowing you to enter the matrix elements.
• Calculation and Results: After inputting your values, click “Calculate.” The tool immediately displays several key metrics:
  • Determinant: The final calculated value.
  • Matrix Size: Confirms the dimensions of your matrix.
  • Singular/Invertible: The tool tells you if the matrix is singular (determinant is 0) or invertible (determinant is non-zero). This is a crucial piece of information in many mathematical contexts.
• Step-by-Step Formulas: The “Steps” section is where this determinant calculator truly shines as a learning aid.
  • For a 2×2 matrix, it displays the classic formula ad - bc and substitutes your values to show how the result was obtained.
  • For a 3×3 matrix, it demonstrates the cofactor expansion method. It breaks down the calculation into finding the determinants of three 2×2 sub-matrices, showing each step clearly.

This function of the matrix determinant calculator not only gives you the answer but also teaches you how to find the determinant of a matrix using standard methods. It’s an invaluable resource for anyone studying or working with linear algebra.

---

🔢
Prime Number Calculator
Check if a number is prime and find factors

Open Calculator →
🎯
GCD/LCM Calculator
Find greatest common divisor and least common multiple

Open Calculator →
📍
Distance Calculator
Calculate distance between two points

Open Calculator →

---

Understanding the Transpose of a Matrix

The transpose of a matrix is a simple yet important operation where the rows and columns are swapped. It’s used in many areas, including data analysis and geometric transformations. The transpose feature in our matrix determinant calculator makes this operation visual and easy to understand.

How to Transpose a Matrix with Our Tool

The process is quick and efficient.

• Inputs: You begin by defining the “Rows” and “Columns” of your original matrix. Unlike other operations, there are no restrictions on the dimensions for a transpose.
• Grid and Controls: An editable grid for your matrix appears. You can enter your values and then use the “Calculate” and “Clear” buttons as needed.
• Metrics and Results: When you click “Calculate,” the tool provides the transposed matrix. It also displays some interesting metrics:
  • Original Matrix Size: Shows the dimensions you started with.
  • Transpose Matrix Size: Shows the new dimensions after swapping rows and columns.
  • Symmetric/Square: The tool will identify if the original matrix is a square matrix (number of rows equals columns) or if it is a symmetric matrix (it is equal to its own transpose).
• Visual Steps: The “Steps” section visually demonstrates the transformation. It shows how the element at row i, column j of the original matrix becomes the element at row j, column i of the transposed matrix. It might show an example like A(2,1) moves to A_T(1,2). This visual aid clarifies the entire process.

This feature of the matrix determinant calculator is perfect for quickly finding the transpose of any matrix and understanding the structural change that occurs.

Practical Use Cases for the Matrix Calculator

Who can benefit from this powerful matrix determinant calculator? The applications are wide-ranging, touching numerous fields of study and professional work. It is more than just a specific determinant calculator; it’s a comprehensive tool for anyone working with matrices.

For Students

Linear algebra is a core subject for students in mathematics, computer science, physics, and engineering. This tool serves as an excellent learning companion. When you’re learning how to find the determinant of a matrix or practicing matrix multiplication, you can use the calculator to check your homework and understand the steps involved. The detailed calculations help bridge the gap between theory and practice, making abstract concepts more concrete. Instead of getting stuck, students can verify their work and build confidence. It can also be useful for more advanced topics, sometimes functioning as a row echelon form calculator in spirit by simplifying complex systems.

For Engineers

Engineers in various disciplines, from electrical to mechanical and civil, frequently use matrices to solve systems of linear equations. For example, in structural analysis, matrices are used to calculate forces and stresses in a building or bridge. In electrical engineering, they are used to analyze circuits. Our matrix determinant calculator allows engineers to quickly perform these calculations without having to rely on cumbersome software or manual work, speeding up their workflow and reducing the chance of errors.

For Mathematicians and Researchers

Mathematicians and researchers often work with complex and large matrices. While they may use advanced software for heavy-duty computation, a quick and accessible online matrix solver like this one is perfect for smaller-scale problems, for checking a hypothesis, or for demonstrating a concept. The clarity of the step-by-step solutions makes it a useful teaching tool in academic settings.

For Programmers and Data Scientists

Programmers, especially those working in graphics and game development, use matrices for transformations like scaling, rotating, and translating objects in 3D space. Data scientists use matrices extensively in algorithms for machine learning, statistical analysis, and data manipulation. This matrix determinant calculator can be a handy utility for debugging an algorithm or quickly calculating a result without writing code.

Whether you’re double-checking a simple 2×2 determinant or multiplying larger matrices for a complex project, the applications are nearly limitless. The tool’s versatility makes it a go-to resource for anyone who encounters matrix operations.

Conclusion

Matrices are a fundamental part of mathematics, science, and engineering, but their calculations can be complex and time-consuming. Our matrix determinant calculator is designed to eliminate these challenges. It offers a clean, intuitive, and powerful platform for performing a wide range of matrix operations.

We have explored its five core functions: addition, subtraction, multiplication, determinant calculation, and transposition. In each section, the tool not only delivers accurate results but also provides detailed, step-by-step explanations that are invaluable for learning and verification. From its role as a matrix solver for complex multiplications to its function as a specific determinant calculator, this tool is built to support a diverse audience.

The clear interface, helpful metrics, and educational focus make it more than just a calculator—it’s a complete resource for matrix mathematics. We encourage you to explore the tool and see how it can simplify your work, enhance your understanding, and boost your productivity.

FAQs