Algebra Calculator: Your Ultimate Online Math-Solving Companion

Introduction

Mathematics can often feel like a foreign language. For many students, staring at a page full of variables, coefficients, and exponents evokes a sense of dread rather than curiosity. Whether you are a high school student tackling algebra for the first time or an adult learner brushing up on skills for a college course, the friction of getting stuck on a single problem can derail an entire study session. This is where a reliable, intuitive tool becomes essential. Enter the Algebra Calculator, a sophisticated yet incredibly accessible online platform designed to bridge the gap between confusion and clarity.

The Algebra Calculator is not just a mechanism for getting answers; it is a comprehensive study companion. Unlike static answer keys in the back of a textbook, this tool provides a dynamic environment where users can input their specific problems and see the logic unfold in real-time. It acts as an online algebra solver that breaks down barriers to understanding, turning what was once a tedious process of trial and error into a streamlined learning experience.

The beauty of this tool lies in its versatility. It doesn’t just handle one type of math problem. It is a multi-faceted hub capable of managing simple linear equations, complex quadratic functions, polynomial factoring, and even the addition or subtraction of lengthy polynomial expressions. By centralizing these distinct mathematical needs into one cohesive interface, the Algebra Calculator saves users the trouble of jumping between different websites or apps.

For students, the value is immediate. Homework sessions that used to take hours can be managed more efficiently. The frustration of getting a “wrong” answer without knowing why is eliminated, as the calculator often provides the context needed to spot mistakes. By serving as a step-by-step equation calculator, it models the correct problem-solving behavior, allowing users to mimic the logic in their future work. It is more than a crutch; it is a scaffold for building genuine mathematical confidence. In the following sections, we will explore exactly how this tool functions, examining every button, input field, and display feature that makes the Algebra Calculator a standout resource for math learners everywhere.

How the Algebra Calculator Interface Works

When you first navigate to the Algebra Calculator, you are greeted by an interface that prioritizes user experience above all else. The design philosophy here is clear: simplicity and focus. The layout is clean, avoiding the cluttered, ad-heavy aesthetic that plagues so many other free online tools. Instead, you find a polished, colorful user interface (UI) that invites interaction rather than overwhelming the senses.

The header of the page sets the tone, often featuring a distinct, readable typeface that clearly identifies the tool. Below this, the core navigation is handled through a series of prominently displayed tabs. These tabs are the control center of the Algebra Calculator. They allow the user to switch seamlessly between different “modes” or mathematical solvers. You aren’t forced to reload the page to switch from solving linear equations to factoring polynomials; a simple click on a tab instantly transforms the workspace to suit the task at hand.

Visually, the tool uses a card-based layout. The active solver sits inside a centralized “card” or container with rounded corners and subtle drop shadows, lifting it off the background and focusing the user’s attention. Input boxes are large and distinct, often highlighted with inviting borders that suggest, “Type here.” The color palette is intentionally chosen to reduce eye strain—soft whites, grays, and blues are common, with brighter accent colors like green or orange reserved for primary actions like the “Solve” buttons.

Interaction is intuitive. There is no hidden menu or complex settings gear to configure. Everything a user needs is right on the surface. When you hover over a button, there might be a subtle color shift, providing immediate visual feedback that the element is clickable. Result cards are initially hidden or empty, appearing only after a calculation is requested, which keeps the interface feeling uncluttered until the information is actually needed.

Furthermore, the Algebra Calculator utilizes distinct visual zones for inputs and outputs. The top half of the active card is always dedicated to user input—this is where you define the problem. The bottom half is strictly for results and analysis. This top-down flow mimics the way we naturally read and solve math problems on paper, making the digital experience feel familiar and organic. The inclusion of metric boxes and step-by-step display areas further enriches the visual landscape, turning a simple answer into a data-rich dashboard of mathematical insight.

Linear Equation Solver Section

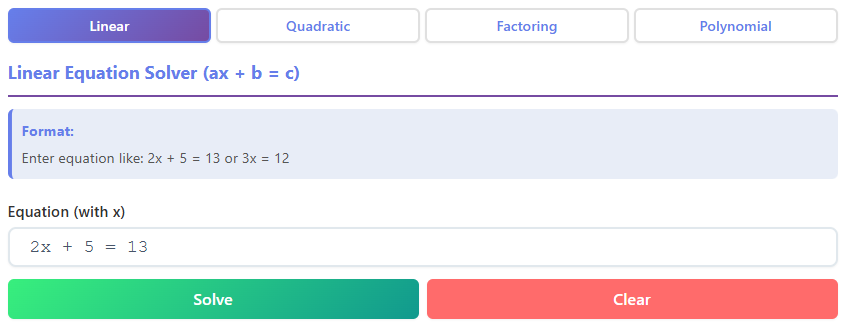
The first tab you encounter is the heartbeat of the Algebra Calculator: the Linear Equation Solver. This section is specifically engineered to handle equations in the format of $ax + b = c$. Upon clicking this tab, the user is presented with a specialized workspace titled “Linear Equation Solver.” The title serves as a helpful reminder of the algebraic structure the tool is expecting, ensuring users know they are in the right place for finding the value of $X$ in standard linear scenarios.

Directly beneath the title, users will notice a helpful instructional tip or “help box.” This small but crucial UI element provides a visual example of what a valid equation looks like, such as “2x + 5 = 13.” This is a thoughtful design touch that prevents user error before it happens. It guides the user on the correct syntax, eliminating the guesswork of wondering whether spaces are allowed or if the variable must be X, Y, or Z.

The center of attention in this section is the primary input bar. It spans the width of the container, offering ample space to type out the equation. The text inside the input field is large and legible, ensuring that typos—like mistaking a plus sign for a minus sign—are easily spotted. As you type, the interface remains responsive, waiting for your command.

To the right or below the input bar, you find the primary action buttons: “Solve” and “Clear.” The “Solve” button is usually emphasized with a bold color, signaling that it is the key to unlocking the answer. Clicking this button triggers the Algebra Calculator to process the input. Conversely, the “Clear” button provides a quick way to reset the field, wiping the slate clean for the next problem without needing to backspace manually.

Once the “Solve” button is clicked, the magic happens in the result card below. This area animates into view or updates instantly. The solution for $X$ is displayed prominently in large, bold text, making the final answer the most visible element on the screen. But the tool goes further. Below the final answer, there is a dedicated “Steps” area. This is where the step-by-step equation calculator functionality shines. It lists out the logical progression: subtracting the constant from both sides, then dividing by the coefficient.

Additionally, users will see “Verification” and “Decimal” metric boxes. The Verification box visually confirms that the calculated answer, when plugged back into the original equation, results in a true statement (e.g., $13 = 13$). This provides peace of mind that the answer is correct. The Decimal metric box offers the solution in decimal format if the result is a fraction, catering to different requirements for science or engineering contexts.

Quadratic Equation Solver Section

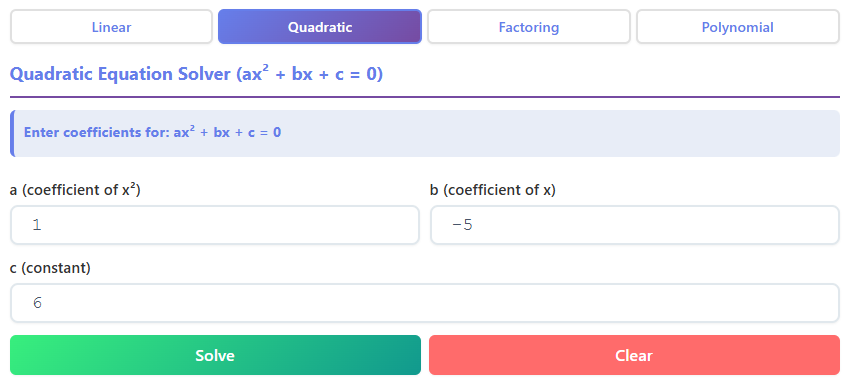
Clicking the second tab transports the user to the Quadratic Equation Solver. This section of the Algebra Calculator is designed to tackle the more complex world of parabolic curves and second-degree polynomials. As a dedicated quadratic equation tool, the layout here shifts slightly to accommodate the specific needs of the standard quadratic form: $ax^2 + bx + c = 0$.

Instead of a single text bar for the whole equation, this interface typically breaks the input down into three distinct fields labeled $a$, $b$, and $c$. This design choice is incredibly user-friendly. It removes the ambiguity of formatting the equation correctly. The user simply identifies the coefficients in their homework problem and types them into the respective boxes. Placeholders inside these boxes might show “1”, “0”, or “-5” as examples, guiding the user on the expected numeric input.

The “Solve” and “Clear” buttons remain consistent with the previous tab, maintaining a sense of continuity across the Algebra Calculator. When the user hits “Solve,” the result card expands to reveal a wealth of information specific to quadratics. Unlike linear equations which usually have one solution, quadratics can have two, one, or none (real ones, at least).

The result area clearly displays the solutions, often labeled as $x1$ and $x2$. If the roots are distinct, both are shown. If it’s a double root, the interface indicates that. But the value of this section extends beyond just the final numbers. A key feature here is the display of the Discriminant value ($b^2 – 4ac$). This specific metric box helps students understand the nature of the roots—whether they are real and distinct, real and equal, or complex.

Furthermore, the Algebra Calculator breaks down the Quadratic Formula itself. Users can see how their inputs ($a$, $b$, and $c$) were plugged into the famous formula. The step-by-step breakdown shows the substitution, the squaring of $b$, the multiplication of $-4ac$, and the final division. This visual walkthrough demystifies the arithmetic, turning a daunting formula into a sequence of simple arithmetic operations. It empowers the user to see exactly where the numbers came from.

Polynomial Factoring Section

The third tab introduces the polynomial factoring calculator functionality. Factoring is often cited by students as one of the most abstract and difficult concepts in algebra to grasp visually. This section of the Algebra Calculator aims to make that process transparent.

The input interface returns to a single, wide bar, similar to the linear solver, but specifically tuned for expressions like $x^2 – 5x + 6$. The prompt invites the user to “Enter Polynomial,” effectively switching the user’s mindset from solving an equation to simplifying an expression.

Upon clicking “Solve,” the result card performs a transformation that feels almost magical to a struggling student. It presents the “Factored Form” in a large, clear font, such as $(x – 2)(x – 3)$. This immediate visual feedback is incredibly satisfying.

Below the main result, the steps list explains how the factorization was achieved. It might highlight the method used, such as “finding two numbers that multiply to 6 and add to -5.” This narrative explanation is vital for learning. It doesn’t just give the answer; it teaches the pattern recognition required for factoring.

Another impressive visual element in this section is the root detection and verification checkmark. The tool often displays the roots associated with the factors (e.g., $x = 2$, $x = 3$) and provides a visual “Verified” badge or checkmark. This signal indicates to the user that the calculator has internally expanded the factored form back into the original polynomial to ensure accuracy. This reliable confirmation builds trust in the Algebra Calculator, assuring the user that the output is mathematically sound.

Polynomial Add/Subtract Section

The fourth tab of the interface is dedicated to the polynomial addition and subtraction solver. While less complex theoretically than factoring, adding and subtracting polynomials is prone to simple arithmetic errors due to the sheer volume of terms and signs involved. This section serves as a meticulous organizer for these lengthy problems.

The layout here is distinct because it requires two separate inputs. Users are presented with two large text fields labeled “Polynomial 1” and “Polynomial 2.” This clear separation helps the user organize their work. They don’t have to worry about parentheses or distributing a negative sign manually in their head before typing; they simply enter the first expression in the top box and the second in the bottom box.

Between these inputs or near the action buttons, there is usually a toggle or a set of distinct buttons for “Add” and “Subtract.” This allows the user to decide the operation without clearing the inputs. You can add two polynomials, see the result, and then immediately click “Subtract” to see the difference between the same two expressions. This flexibility is excellent for comparing results.

The result card here is particularly focused on “Like Terms.” When the calculation is displayed, the Algebra Calculator often groups the answer by the power of the variable (e.g., all $x^2$ terms combined, all $x$ terms combined). The “Calculation” steps area is invaluable here. It visually demonstrates the grouping process. It might show the raw combination of Polynomial 1 and Polynomial 2, followed by a line where the terms are reordered, and finally the simplified result.

For students, this visual grouping is a game-changer. It highlights the importance of organization in algebra. seeing the terms physically move and combine on the screen reinforces the rules of combining like terms better than static text ever could. It turns a messy problem into a tidy, ordered solution.

Why This Algebra Calculator Is Helpful

The utility of the Algebra Calculator extends far beyond simply getting the right answer. In an educational landscape that is increasingly digital, having a reliable online algebra solver is akin to having a tutor available 24/7. One of the primary benefits is the immediacy of the solution. When a student is stuck on a problem at 11 PM, they don’t have to wait until class the next day to get unblocked. The calculator provides instant feedback, keeping the momentum of study alive.

However, speed is nothing without understanding. The true power of this tool lies in its role as a step-by-step equation calculator. By showing the work—whether it is the substitution in the quadratic formula or the grouping of terms in polynomial addition—the calculator demystifies the process. It allows students to reverse-engineer the solution, comparing their own manual work line-by-line with the calculator’s output to find exactly where they went wrong. This active form of error correction is one of the most effective ways to learn.

The Algebra Calculator is also a champion of accuracy. Human error is natural; dropping a negative sign or miscalculating $7 \times 6$ happens to the best of us. This tool provides an error-free baseline. For students checking their homework, it offers the reassurance that their answers are correct, boosting their confidence before a test.

Moreover, the versatility of having a quadratic equation tool, a polynomial factoring calculator, and a polynomial addition and subtraction solver all in one place cannot be overstated. It streamlines the workflow. Students can tackle a mixed review sheet involving various types of algebra problems without ever leaving the page. The consistent interface means they don’t have to relearn how to use the tool for every new topic; the button placement and logic remain familiar, allowing them to focus entirely on the math.

Conclusion

In the journey of mastering mathematics, having the right tools can make all the difference between frustration and success. The Algebra Calculator stands out as a premier resource for students, parents, and lifelong learners alike. Its thoughtfully designed interface, which prioritizes clarity and ease of use, removes the intimidation factor often associated with algebra. From the straightforward layout of the linear solver to the multi-field precision of the quadratic section, every pixel of the tool is engineered to support the user’s understanding.

By offering a robust suite of features—including an intuitive online algebra solver, a detailed step-by-step equation calculator, and specialized modes for quadratics and polynomials—the Algebra Calculator adapts to the diverse needs of the math curriculum. It doesn’t just hand out answers; it illuminates the path to the solution. Whether you are using it to verify a difficult factoring problem or to ensure your polynomial subtraction is sign-perfect, this tool is an indispensable ally. Embrace the power of digital assistance and let the Algebra Calculator transform the way you approach, solve, and understand algebra today.

---

FAQs