Number System Converter: Your Ultimate Guide to Accurate Conversions

In our digitally driven world, numbers are the fundamental language that powers everything from complex software to the simplest electronic devices. However, not all numbers are represented in the same way. Different contexts require different numerical systems. This is where a number system converter becomes an indispensable tool. At its core, a number system converter is a utility designed to translate a number from one base system to another without altering its value. This process is crucial in fields like computing, electronics, programming, and even education, where understanding and manipulating data across various formats is a daily requirement.

The most common number systems you’ll encounter are Binary (base-2), Decimal (base-10), Hexadecimal (base-16), and Octal (base-8). While we use the decimal system for everyday counting, computers operate using binary. Programmers often use hexadecimal and octal to represent binary data more concisely. The ability to switch between these systems is not just a convenience; it’s a necessity for clarity, efficiency, and error prevention. Accurate conversion ensures that the data’s integrity is maintained, whether you’re debugging code, designing a circuit, or learning the principles of computer science.

A reliable number system converter bridges the gap between human-readable numbers and the machine language that underpins our technological landscape. For students and professionals alike, mastering the use of a high-quality number system converter is a key skill. This guide will walk you through a powerful and user-friendly number system converter designed to make these conversions seamless and precise.

Understanding the Core Number Systems

Before diving into the tool itself, let’s briefly touch upon the systems it handles. Each system uses a different set of symbols and a different base to represent numerical values.

Decimal (Base-10)

This is the system we learn from childhood. It uses ten digits (0-9) to represent any number. Each position in a decimal number represents a power of 10. It is the universal standard for human communication of quantity.

Binary (Base-2)

The language of computers. The binary system uses only two digits: 0 and 1. These are often referred to as “bits.” Each position in a binary number represents a power of 2. While simple in its components, binary sequences can become very long, making them cumbersome for humans to read and write.

Hexadecimal (Base-16)

To simplify long binary strings, programmers often turn to hexadecimal. This system uses 16 symbols: the digits 0-9 and the letters A-F (where A represents 10, B is 11, and so on up to F for 15). Because 16 is a power of 2 (2^4), a single hexadecimal digit can represent a four-digit binary number, making it a much more compact notation.

Octal (Base-8)

Similar to hexadecimal, the octal system provides a more concise way to represent binary numbers. It uses eight digits (0-7). Since 8 is also a power of 2 (2^3), one octal digit can represent a three-digit binary number. Though less common today than hexadecimal, it still has applications in certain computing systems, particularly in file permissions on UNIX-like systems.

The need to translate values between these systems is constant in technical fields. A robust number system converter removes the manual effort and potential for human error from these critical tasks, providing instant and accurate results every time.

🔢 Number System Converter: A Tool Overview

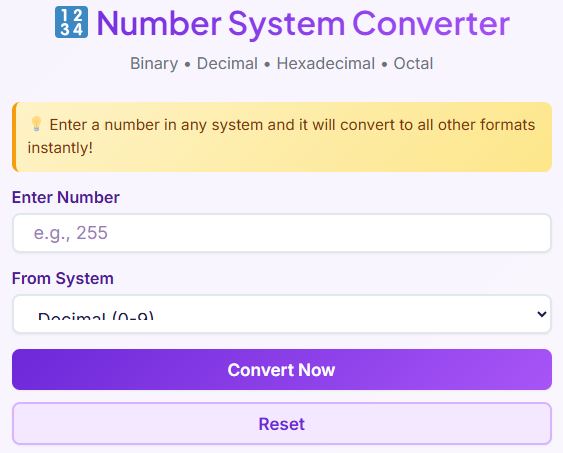
Welcome to the ultimate tool for seamless numerical translations. The number system converter is more than just a calculator; it’s a comprehensive solution for anyone working with different number bases.

This tool is designed to handle conversions between the four most essential systems: Binary, Decimal, Hexadecimal, and Octal. Its clean and modern interface, featuring a subtle gradient design, is not only visually appealing but also highly intuitive. We built this number system converter with the user experience as the top priority.

The tool is fully responsive, ensuring a flawless experience whether you are on a desktop computer, a tablet, or a mobile phone. This flexibility allows you to perform conversions on the go, right when you need them. The layout is simple and uncluttered, guiding you through the conversion process without any confusion. There are no complex menus or hidden options; everything you need is presented clearly on the screen.

The primary goal of this online number system converter is to provide a fast, reliable, and user-friendly platform for all your conversion needs, removing the complexity and leaving you with pure, accurate results. Its ease of use makes it suitable for both seasoned professionals and students who are just beginning their journey into computer science and electronics.

The Input Section: Your Starting Point

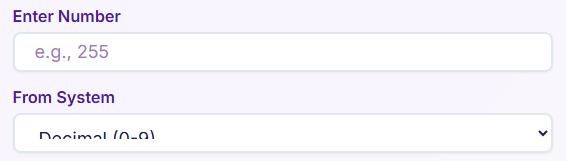
The conversion process begins with the input section, which is designed for clarity and ease of use. This is where you provide the number you wish to convert. The simplicity of this section ensures that you can get started immediately, without a learning curve. The core of the input area consists of two main elements that work together to define your conversion task. Using this section of the number system converter is straightforward.

Enter Your Number

The first element is a prominent input field labeled “Enter Number”. This is a standard text box where you type or paste the numerical value you want to convert. For instance, if you want to convert the decimal number 255, you simply type “255” into this box. The field is designed to accept a wide range of characters to accommodate the different number systems. For hexadecimal, it accepts letters A-F in addition to digits. This flexibility is key to making the number system converter a truly versatile utility. It’s a simple yet powerful starting point for any conversion.

Select the “From System”

Directly below the number field, you’ll find the “From System” dropdown menu. This crucial step tells the number system converter what base your input number is in. The menu provides four clear options:

• Decimal (Base 10)
• Binary (Base 2)
• Hexadecimal (Base 16)
• Octal (Base 8)

You must select the system that corresponds to the number you entered. For example, if you entered “11111111”, you need to specify whether this is a binary number or a decimal number. The tool provides real-time guidance to help you avoid mistakes. If you try to select “Binary” but have entered a character like “2” or “A”, the tool will alert you to the incompatibility later in the process. This intelligent validation makes the entire experience smoother and more reliable. This section is also versatile enough to support tasks that go beyond simple numbers, forming a foundational step for tools like a binary addition calculator or even a conceptual words to numbers converter.

The Convert Button: Instantaneous Results

Once you have entered your number and selected its original base system, the magic happens with a single click. The “Convert Now” button is the engine of the number system converter, executing the complex logic of base conversion instantly and presenting the results in a clean, organized format. This button is designed for immediate action, providing the answers you need without any delay.

Activating the Conversion

When you press the “Convert Now” button, the tool takes your input value and the “From System” selection and processes them. Behind the scenes, it translates the number into its equivalent in the other three number systems. For example, if you enter the decimal number “10” and click convert, the number system converter will immediately calculate its binary, hexadecimal, and octal equivalents. This instant feedback loop is essential for productivity, especially when you need to perform multiple conversions quickly.

Dynamic Result Display

The results are not just displayed as plain text. Instead, they appear dynamically in a series of well-designed, separate cards, one for each number system. This organized presentation allows you to see all the conversions at a glance, making it easy to compare the different representations of the same value. Whether you are converting decimal to binary for a class assignment or need a quick hexadecimal value for a CSS color code, the results are clear and unambiguous. The seamless transition from input to output showcases the efficiency of this powerful number system converter. This function is what makes it an excellent binary number converter and so much more, providing a comprehensive view of a number’s identity across different bases.

The Reset Button: A Clean Slate

After performing a conversion, you may need to start over with a new number. To make this process as efficient as possible, the tool includes a dedicated “Reset” button. This simple but essential feature is designed to clear the slate and prepare the interface for your next task with a single click. It’s another example of how the number system converter prioritizes user convenience.

Clearing Inputs and Results

When you click the “Reset” button, it performs two main actions. First, it completely clears the “Enter Number” input field, so you don’t have to manually delete the previous entry. Second, it removes all the result cards that were generated from the previous conversion. The screen returns to its original state, ready for fresh input. This prevents confusion and ensures that you are always working with a clean workspace. This functionality is crucial for maintaining a smooth workflow, especially during sessions involving numerous, unrelated conversions.

Resetting Focus for Convenience

In addition to clearing the fields, the reset function also automatically places the cursor’s focus back into the “Enter Number” input box. This might seem like a small detail, but it significantly improves the user experience. You don’t have to click back into the box to start typing your next number; you can simply hit “Reset” and immediately begin entering the new value. This thoughtful design element streamlines the process, saving you clicks and time. It reinforces the idea that every aspect of this number system converter was built with the user’s workflow in mind.

The Results Section: Clarity and Precision

The output of any conversion tool is its most critical component, and the number system converter excels in delivering results with exceptional clarity and precision. Instead of a simple list of numbers, the tool presents the conversions in a visually organized and highly functional results section. This is where the power of the tool truly shines, providing you with the data you need in a format that is both easy to read and practical to use. This makes it far more than a basic calculator; it is a comprehensive information hub.

Organized Column Layout

Upon conversion, the results are displayed in a neat column layout. Each of the four number systems—Decimal, Binary, Hexadecimal, and Octal—gets its own dedicated result card. This structure allows for quick side-by-side comparison. You can instantly see how a single value, such as the number 255, is represented across all four bases. This clear separation prevents any confusion and makes the information easy to digest at a glance.

Detailed Result Cards

Each result card is meticulously designed for maximum utility. It includes:

• An Emoji and Label: A small icon and a clear label (e.g., “HEX” for Hexadecimal) identify the number system at a glance.
• The Converted Value: The main feature of the card is the converted number itself, displayed in a large, legible font. For example, when you convert the decimal number 2, the binary card will prominently display “10”. This makes finding simple values like 2 in binary effortless.
• A “Copy” Button: To the right of the converted value is a convenient copy button. A single click on this button copies the number directly to your clipboard, ready to be pasted into your code, a document, or any other application. This eliminates the need for manual selection and copying, reducing the risk of errors and speeding up your workflow.

This section turns the number system converter into a productivity tool. It can even handle conceptual tasks, providing a structured output that could be adapted for a words to numbers converter if the inputs were properly mapped. The precision of the results is guaranteed, ensuring that whether you are a student or a professional, you can trust the output of this number system converter. The intuitive design of the results section solidifies the utility of this exceptional number system converter.

Smart Error Handling for a Better Experience

A truly great tool not only performs its primary function well but also guides the user and helps them avoid mistakes. The number system converter is equipped with intelligent error-handling capabilities that enhance the user experience by providing clear, real-time feedback when something goes wrong. This proactive approach prevents user frustration and ensures that the conversions are always based on valid data.

Alerts for Invalid Input

The tool is smart enough to know which characters are valid for each number system. For example, the binary system can only contain the digits 0 and 1. If you accidentally enter the number “102” and then select “Binary” as the “From System,” the tool will recognize that “2” is not a valid binary digit. Instead of producing a nonsensical result or crashing, the number system converter will display a helpful alert. This message will inform you that the input is invalid for the selected number system, prompting you to correct it.

Compatibility Warnings

This error checking ensures that the logic of the number systems is respected. A hexadecimal number can contain letters from A to F, but a decimal number cannot. An octal number cannot contain the digits 8 or 9. The tool validates your input against the rules of your chosen base system. This validation step is crucial for maintaining the integrity of the conversions. By catching these errors upfront, the tool saves you time and prevents the propagation of incorrect data into your work. This thoughtful error-handling mechanism is a testament to the user-centric design of the number system converter, making it a more reliable and friendly utility for everyone.

Real-Life Use Cases and Applications

A number system converter is not just an abstract utility for mathematicians; it has tangible, real-world applications across a wide range of technical and educational fields. Professionals and students alike rely on accurate base conversions to perform their daily tasks efficiently and correctly. The versatility of a powerful number system converter makes it an essential part of any digital toolkit.

For Programmers and Software Developers

Programmers constantly work with different number representations. When debugging low-level code, they might analyze memory dumps displayed in hexadecimal. They use binary to perform bitwise operations, which are fundamental in areas like graphics programming, networking, and encryption. For instance, a developer might use a binary addition calculator to manually verify the result of a bitwise OR operation. The ability to quickly switch between decimal, binary, and hexadecimal is crucial for writing and optimizing code. A reliable number system converter streamlines this process, allowing them to focus on logic rather than manual arithmetic.

For Computer Science Students

Learning about computer architecture and data representation is a cornerstone of any computer science curriculum. Students are often tasked with homework and exam problems that involve converting decimal to binary and back. Understanding how a number like 255 is represented as 11111111 in binary is a fundamental concept. A number system converter serves as an excellent learning aid, allowing students to check their manual calculations and gain a more intuitive understanding of how different bases work. It can help them visualize the relationship between the systems and solidify their knowledge.

For Electronics Engineers and Technicians

In the world of electronics and hardware design, binary is the language of digital circuits. Engineers designing logic gates or working with microcontrollers need to think in binary. They use a binary number converter to translate specifications and data sheet values into the binary sequences that control hardware behavior. Hexadecimal is also commonly used as a shorthand for configuring registers or setting memory addresses. An accurate number system converter is an indispensable tool on the bench of any electronics professional.

For Data Analysts and Writers

The concept of converting between representations extends beyond traditional number systems. In finance, legal fields, or automated content generation, there’s often a need for a words to numbers converter. This involves translating numerical digits (e.g., “1,200”) into their word form (“one thousand two hundred”) for formal documents or checks. While our tool focuses on numerical bases, the underlying principle of translation is similar, highlighting the broad applicability of conversion utilities in modern workflows.

Expanding Your Toolkit with Internal Links

Mastering conversions is a key skill, but many projects require a diverse set of tools. Just as a reliable number system converter is essential for handling numerical bases, other specialized converters can save you significant time and effort in different domains. Integrating these tools into your workflow can boost productivity and ensure accuracy across all your tasks. Here are a few other powerful converters that you might find useful.

If you work with international teams or plan travel, managing time differences can be a constant challenge. Instead of manually calculating offsets, a dedicated tool can provide instant and accurate answers.
🌐 Timezone Converter – Convert between world time zones
Open Converter →

Shopping online from international retailers often involves confusion over sizing. What is a size 8 in the US might be a 10 in the UK or a 40 in Europe. A converter that specializes in apparel can eliminate the guesswork.
👕 Clothing Size Converter – Convert US, UK, EU clothing sizes
Open Converter →

For anyone who enjoys cooking or baking, translating recipes from different measurement systems can be tricky. Converting between metric and imperial units like cups, tablespoons, and grams requires precision for the best results.
🍳 Cooking Converter – Convert cups, tablespoons, teaspoons
Open Converter →

Having a suite of reliable tools at your disposal, from a number system converter to a cooking converter, empowers you to handle any conversion task with confidence and speed.

Conclusion: Your Go-To Conversion Solution

Navigating the complexities of different numerical bases is a common challenge in many technical and academic fields. The number system converter we’ve explored is designed to eliminate that complexity entirely. Its user-friendly interface, combined with powerful, real-time conversion capabilities, makes it the ideal tool for anyone who needs to translate numbers between decimal, binary, hexadecimal, and octal systems. The emphasis on accuracy, speed, and a seamless user experience ensures that you get reliable results instantly, every time.

From its intuitive input fields and dynamic result cards to its intelligent error handling, every aspect of this tool has been crafted with the user’s needs in mind. Its global applicability makes it an invaluable asset for students learning the fundamentals of computer science, programmers debugging complex code, and engineers designing digital circuits. We encourage you to bookmark this number system converter and make it a regular part of your digital toolkit. Experience the ease and precision of effortless number conversions today.

FAQs